Given
A circles passes through A(8,4) and B(0,-2).
To find the radius and the equation of the circle.
Step-by-step explanation:
It is given that,
A circles passes through (8,4) and (0,-2).
Then, the diameter of the circle is,
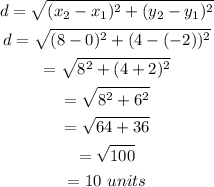
Therefore, the radius of the circle is,
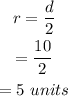
Also, the center of the circle is,
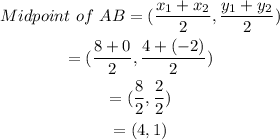
Therefore, the center is (4,1).
Now, consider the equation of the circle as,
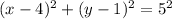
That implies,
![undefined]()