Question

The graph below shows a company’s profit f(x) in dollars depending on the price of pens x, in dollars, sold by the company What do the x-intercepts and maximum value of the graph represent? What are the intervals where the function is increasing and decreasing and what do they represent about the sale and profit? What is an aproxímate average rate of change of the graph from x=3 to x=5 and what does this rate represent?

Answer 1

Given:

`\begin{gathered} f(x)=profits \\ x=price\text{ of pens} \end{gathered}`

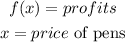
From the graph, the x-intercept exists at (0,0) and (6,0).

The maximum value is (3,120).

The x-intercept represents the break-even points. The company was not in profit or loss when no pen was sold and when 6 pens were sold, the profit was $0 at these two points.

The maximum value of the graph represents the maximum profit made by the company. The company made a maximum profit of $120 when 3 pens were sold.

The interval where the function is increasing is from negative infinity to x = 3. This shows that the more pen sold, the higher the profit made.

The interval where the function is decreasing is from x = 3 to positive infinity. This shows that the less pen sold, the lower the profit made.

The approximate average rate of change of the graph from x = 3 to x = 5 is;

`\begin{gathered} ARC=(f(x_2)-f(x_1))/(x_2-x_1) \\ where: \\ x_1=3 \\ x_2=5 \\ f(x_1)=120 \\ f(x_2)=60 \\ \\ Hence, \\ ARC=(60-120)/(5-3) \\ ARC=(-60)/(2) \\ ARC=-30 \end{gathered}`

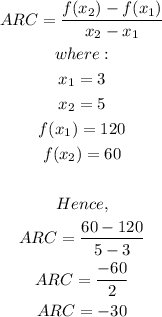
The rate represents a decrease of $30 for every pen sold across the decreasing interval.