Answer:
The number of seconds required to complete 7 revolutions is 236.28 s.
Explanation:
Given;
speed of the point on the wheel, ω = 32π/9 rad/min
number of revolutions made by the point, θ = 7 rev
The time taken for the point to make 7 revolutions is calculated as follows;
1 rev = 2π rad
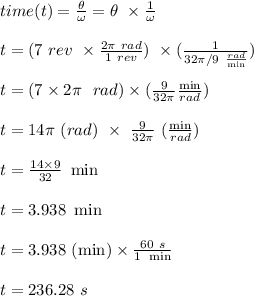
Therefor, the number of seconds required to complete 7 revolutions is 236.28 s.