Question

A sequence starts with: 44, 176, 704, 2816... Calculate the next 4 terms. 0 SCH

Answer 1

Since the terms of the sequence are increasing with large magnitudes (with a multiplicative factor of 4), it appears to be a geometric sequence.

As such, we have the first term to be:

`a=44`

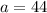
and the common ratio is:

`r=(176)/(44)=4`

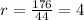
Now, given that the nth term of a geometric sequence is given by:

`T_n=ar^(n-1)`

Thus, the fifth term is:

`\begin{gathered} T_5=ar^(n-1) \\ T_5=(44)*(4)^(5-1) \\ T_5=(44)*(4)^4 \\ T_5=(44)*(256) \\ T_5=11264 \end{gathered}`

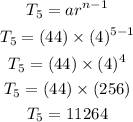
Also, the sixth term is: