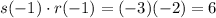Question

Suppose that the functions and s are defined for all real numbers x as follows.r(x) = 3x+1s(x)=x-2Write the expressions for (s-r) (x) and (s+r)(x) and evaluate (s.r) (-1).(sr)(x) = [(s+r)(x) = [(sr)(-1) =XS

Answer 1

In this problem, we are doing combinations of functions.

This means that we can carry out various operations with functions, including adding, subtracting, multiplying, and dividing.

We are given the following functions:

`\begin{gathered} r(x)=3x+1 \\ \\ s(x)=x-2 \end{gathered}`

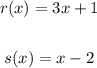
Part 1:

In the first part of the question, we want to evaluate:

`(s-r)(x)`

By definition, this means we will do:

`s(x)-r(x)`

Substituting the functions gives us:

`s(x)-r(x)=(x-2)-(3x+1)`

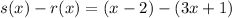
Now we can simplify as if we are combining like terms. First, distribute the negative to the second expression:

`\begin{gathered} (x-2)-(3x+1) \\ \\ x-2-(3x)-(1) \\ \\ x-2-3x-1 \end{gathered}`

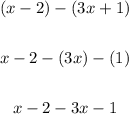
Combine like terms:

`-2x-3`

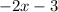
So,

`(s-r)(x)=-2x-3`

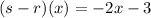
Part 2:

Next, we want to find:

`(s+r)(x)=s(x)+r(x)`

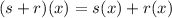
Substituting our functions gives us:

`(x-2)+(3x+1)`

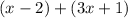
Drop the parentheses and combine like terms:

`\begin{gathered} x-2+3x+1 \\ \\ 4x-1 \end{gathered}`

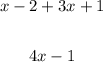
Therefore,

`(s+r)(x)=4x-1`

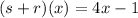
Part 3:

Finally, we want to evaluate:

`(s\cdot r)(-1)=s(-1)\cdot r(-1)`

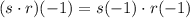
Evaluating s(-1), we get:

`s(-1)=-1-2=-3`

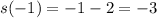
Then evaluating r(-1) gives us:

`r(-1)=3(-1)+1=-2`

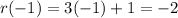
Substituting these values leads to the final answer:

`s(-1)\cdot r(-1)=(-3)(-2)=6`