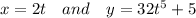We are given the following equation
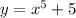
We are asked to find two different parametric equations for the above equation.
There are many different possibilities to write the parametric equations.
For example:
Let x = t and substitute it into the given equation
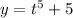
So, we have got a set of parametric equations
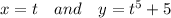
Similarly,
Let x = 2t and substitute it into the given equation
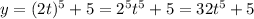
So, we have got another set of parametric equations