Question

A store's sales grow according to the recursive rule Pn = Pn-1 + 12000, with initial sales Po = 27000.(a) Calculate and P2.P1 = $P2 = $(b) Find an explicit formula for Pr.Pn-(c) Use the explicit formula to predict the store's sales in 10 years.P10 = $(d) When will the store's sales exceed $97,000? Round your answer to the nearest tenth of a year.Afteryears.Anetails

Answer 1

22270d

1) Since the sales have been modeled by this recursive formula, we need to make reference to the prior item in the sequence to find the next one:

a) P_1 and P_2

`\begin{gathered} P_n=P_(n-1)+12000 \\ P_1=27000+12000 \\ P_1=39000 \\ --- \\ P_2=39000+12000 \\ P_2=51000 \end{gathered}`

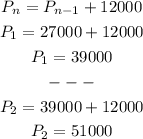
Note that whenever we have a recursive formula we'll need the prior item to get the subsequent one.

b) Explicit formula for P_N

When we have an explicit formula, we don't need the prior term. So let's find an explicit one:

`P_N=27000+12000N`

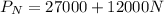
Note that the difference between P_2 and P_1 is 12,000.

c) Now, let's pick this explicit formula and find P_10:

`\begin{gathered} P_(10)=27000+12000\cdot10 \\ P_(10)=147,000 \end{gathered}`

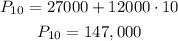
d) Let's use the explicit formula to find when, in years the store is going to exceed 97000

97000=27000+12