Question

An objects height varies directly with the length of its shadow. A person who is 6 feet tall casts a 15-foot shadow. How long is the shadow of a 20-foot tree?

Answer 1

Step-by-step explanation

If the height of an object h varies directly with the length of its shadow l then both quantities are related by an expression like this one:

`h=k\cdot l`

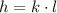
Where k is a number. We are told that a 6 ft tall person has a 15 ft long shadow. This means that for h=6 we have l=15. Then we can construct an equation for k:

`6=15k`

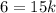
We can divide both sides by 15:

`\begin{gathered} (6)/(15)=(15k)/(15) \\ k=(2)/(5)=0.4 \end{gathered}`

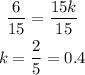
So the relation between height and the length of the shadow is:

`h=0.4l`

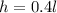
Then if the tree is 20 ft tall we get:

`20=0.4l`

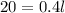
We can divide both sides by 0.4:

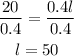
`\begin{gathered} (20)/(0.4)=(0.4l)/(0.4) \\ l=50 \end{gathered}`Answer

Then the answer is 50 ft.