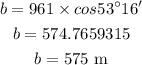To solve a right triangle means to find all unknown angles and sides
From the given figure we can seeL
A right triangle ABC, where
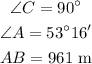
Since the sum of angles of a triangle is 180 degrees, then we can find angle B by subtraction angles C and A from 180
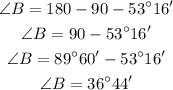
To find a and b, we will use the trigonometry ratios sine and cosine

By using the cross multiplication
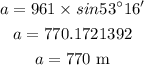
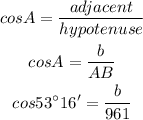
By using the cross multiplication