Question

Select the correct answer from each drop-down menu. Consider polynomial functionſ. f(t) = (x - 1)(x + 3)(x + 1) a Use the equation to complete each statement about this function. 3 has a multiplicity of The zero located at t = 1 has a multiplicity of and the zero located at 1 The graph of the function will touch, but not cross, the x axls at an x-value of

Answer 1

Question:

Solution:

Consider the following function:

`f(x)=(x-1)^2(x+3)^3(x+1)`

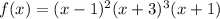
The number of times a given factor appears in the factored form of the equation of a polynomial is called multiplicity.

The zero that is associated with the factor (x-1) is x=1 and it has multiplicity 2 because the factor (x-1) occurs twice.

Now, the zero that is associated with the factor (x+3) os x= -3, and it has multiplicity 3 because the factor (x+3) occurs three times.

Now, the graph of this function is:

According to this graph, we can conclude that the graph of the function will touch, but not cross, the x-axis at an x-value of x= 1.

So that, we can conclude that the correct answers are:

The zero located at x = 1 has a multiplicity of 2.

The zero located at x=-3 has a multiplicity of 3.

The graph of the function will touch, but not cross, the x-axis

at an x-value of​ 1.