We have a rectangular prism.
The surface area is the sum of the area of the faces.
We have 3 pairs of faces. Each pair has two pair of measures for the sides, so, if the sides are a=12, b=12 and c=25, we can calculate the surface area as:
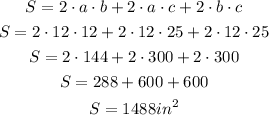
Answer: the surface area is 1488 square inches.
NOTE: if we want the surface in square feet we can do:
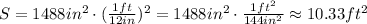
The surface area is approximately 10.33 square feet.