Question

018You weigh 740 N.What would you weigh if the Earth weretwo times as massive as it is and its radiuswere four times its present value?

Answer 1

Given that the weight of the person is W = 740 N.

The weight can be calculated by the formula,

`\begin{gathered} W=mg \\ m\text{ =}(W)/(g) \end{gathered}`

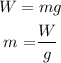
Here, m is the mass of the person, g is the acceleration due to the gravity of the earth.

`\begin{gathered} g\text{ = }(GM)/(R^2) \\ =(9.81m)/(s^2) \end{gathered}`

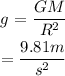
Here, G is the universal gravitational constant.

M is the mass of the earth and R is the radius of the earth.

The mass of the person will be

`\begin{gathered} m\text{ = }(740)/(9.81) \\ =75.43\text{ kg} \end{gathered}`

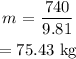
Now, the new acceleration due to gravity is

`\begin{gathered} g^(\prime)=(2GM)/((4R)^2) \\ =(2)/(16)* g \\ =1.226m/s^2 \end{gathered}`

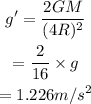
Now the new weight will be

`\begin{gathered} W^(\prime)\text{ = m}* g^(\prime) \\ =\text{ 75.43}*1.226 \\ =92.477\text{ N} \end{gathered}`

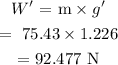
Thus, the new weight is 92.477 N.