Question

Martha conducted an experiment in which shedropped marbles into a beaker that containedsomewater. As each marble was added, the waterlevel in the beaker was recorded in a table.Note: eachmarble was identical in size and material as thenext. Unfortunately, she spilled water on herdatatable and the water dissolved all her informationexcept for two data points: (5 marbles, 22milliliters) and (12 marbles, 50 milliliters). Usingwhat is left of the data, answer the followingquestionsA) How much did the water rise each time amarble was added to the beaker? How do youknow?B) What was the height of the water in thebeaker before Martha started adding marbles?How do you know?C)Write an equation Martha can use to predict theheight of the water if she knows how manymarbles have been added.

Answer 1

To solve this problem, we will be using linear equation. This is appropriate given that we only have 2 points and the problem specifies that each marble is identical in size, meaning the water rises at the same rate.

Let's identify the x and the y--our independent and dependent variables.

The independent variable here is the input--the number of marbles (5 and 12), while the dependent variable is the output--the volume reading on the beaker (22 and 50).

So we have the points (5, 22) and (12, 50).

Let's solve for the slope, m.

`\begin{gathered} m=(y_1-y_2)/(x_1-x_2) \\ \\ m=(22-50)/(5-12) \\ \\ m=(-28)/(-7) \\ \\ m=4 \end{gathered}`

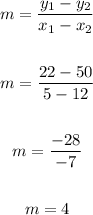
This also gives us the rise of water each time that a marble is added--4mL.

Then, we use one of the points to solve the y-intercept b. let's use (5, 22).

`\begin{gathered} y=mx+b \\ \\ 22=4(5)+b \\ \\ 22=20+b \\ \\ 2=b \end{gathered}`

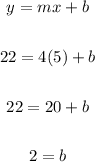
So the equation that Martha can use to predict the height of the water is:

y = 4x + 2

Knowing this, we can solve for when x = 0 to find the height of the water before Martha added marbles.

`\begin{gathered} y=4x+2 \\ y=4(0)+2 \\ y=2 \end{gathered}`

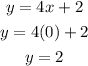
The height of the water in the beaker before Martha started adding marbles was 2 mL.