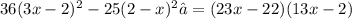Factorize the following function 36(3x-2)² - 25(2-x)²

Question

asked Apr 22, 2023 88.8k views

1 Answer

Grzegorz Herman · Answer 1 · 2023-04-28T19:54:27+0000

The question is given to factorize the expression:

$36\mleft(3x-2\mright)^2\: -\: 25\mleft(2-x\mright)^2$

Given that:

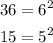
$\begin{gathered} 36=6^2 \\ 15=5^2 \end{gathered}$

Therefore, the expression becomes:

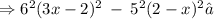
$\Rightarrow6^2(3x-2)^2\: -\: 5^2(2-x)^2$

Recall the rule of exponents:

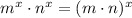
$m^x\cdot n^x=(m\cdot n)^x$

Hence, the expression can be rewritten to be:

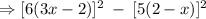
$\Rightarrow\lbrack6(3x-2)\rbrack^2\: -\: \lbrack5(2-x)\rbrack^2$

Expand the terms in the brackets:

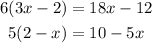
$\begin{gathered} 6(3x-2)=18x-12 \\ 5(2-x)=10-5x \end{gathered}$

Hence, we have the expression to be:

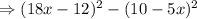
$\Rightarrow(18x-12)^2-(10-5x)^2$

Recall the Difference of Two Squares Formula, defined as:

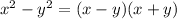
Hence, we have the expression to be:

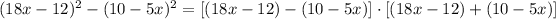
$(18x-12)^2-(10-5x)^2=\lbrack(18x-12)-(10-5x)\rbrack\cdot\lbrack(18x-12)+(10-5x)\rbrack$

Simplifying, we have:

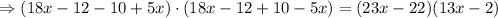
$\Rightarrow(18x-12-10+5x)\cdot(18x-12+10-5x)=(23x-22)(13x-2)$

ANSWER:

$36\mleft(3x-2\mright)^(2)-25\mleft(2-x\mright)^(2)=(23x-22)(13x-2)$