Explanation:
Exponential function:
In the following format:
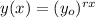
r is the rate of change.
The domain is: x >= 0
The maximum is y(0).
The minimum is close to 0.
In this question:
The average value is $30,750. So the function can be modeled as:
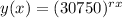
The graph is positive for all values of x.
The domain of the function is x >= 0
The maximum is y = $30,750
The minimum is close to 0.