We are asked to determine the decay constant of a radioactive element. To do that we will use the following formula:
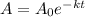
Where:

The half time is the time when the quantity of the element is half the initial quantity. Therefore, we have:
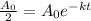
Now, we cancel out the initial quantitu:
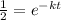
Now, we solve for "t". First, we take the natural logarithm to both sides:
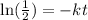
Now, we divide both sides by -t:
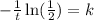
Now, we plug in the value of the time:
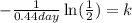
Solving the operations:
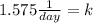
Therefore, the decay constant is 1.575 1/day.