Answer:
x = 1.3863
Step-by-step explanation:
We can rewrite our equation as
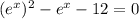
which can be factored as
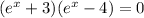
Therefore, the two equations we must solve are
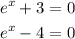
The first equation gives
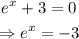
Since the natural logarithm can never give a negative number, the above equation is undefined.
Now the second equation gives
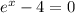
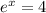
taking the natural log of both sides gives
![\ln[e^x]=\ln[4]](https://img.qammunity.org/2023/formulas/mathematics/college/topzrbi0ca4333ow97a1j4klo8pqjypsf4.png)
![\boxed{x=\ln[4].}](https://img.qammunity.org/2023/formulas/mathematics/college/30vgs9cpt3xlwtaberaqwqjzfdjt0ez1oe.png)
which we evaluate to get (rounded to the nearest four decimal places)
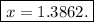
which is our answer!