Question

Monya and Kishi are hiking in the mountains and stop for lunch on a ledge 1000 feet above the valley below. Kishi decides to climb to another ledge 20 feet above Monya. Monya throws an apple up to Kishi, but Kishi misses it. The function h(t) = -16t2 + 30t + 1000 represents the height in feet of the apple at any given time in seconds.1. What is the maximum height of the apple? 2. How long did it take the apple to reach the maximum height? 3. How long did it take for the apple to hit the ground?

Answer 1

1) The function given is a quadratic function with negative leading coefficient, so its maximum value can be calculated using the formula for the y value of the vertex of a parabola:

`\begin{gathered} y_v=-(\Delta)/(4a) \\ \Delta=b^2-4ac \end{gathered}`

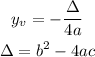
Since the function is give, we can get the values for a, b and c:

`\begin{gathered} y=ax^2+bx+c \\ h(t)=-16t^2+30t+1000 \end{gathered}`

So:

`\begin{gathered} \Delta=30^2-4(-16)(1000)=900+64000=64900 \\ h_(\max )=-(64900)/(4(-16))=-(64900)/(-64)=1014.0625 \end{gathered}`

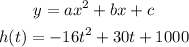
So, the maximum height is 1014.0625 feet.

2) This is also the vertex of the parabola, but now the x value formula:

`x_v=-(b)/(2a)`

So:

`t_(\max )=-(30)/(2(-16))=-(30)/(-32)=0.9375`

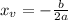
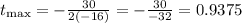
So, it take 0.9375 seconds to reach the maximum.

3) When it hits the ground, h(t) = 0, so this is the same as fiding the zero of the function, which we can do by using the quadratic formula:

`\begin{gathered} t=\frac{-b\pm\sqrt[]{\Delta}}{2a}=\frac{-30\pm\sqrt[]{64900}}{2(-16)}=(-30\pm254.754\ldots)/(-32) \\ t_1=(-30+254.754\ldots)/(-32)=(224.754\ldots)/(-32)=-7.02358\ldots \\ t_2=(-30-254.754\ldots)/(-32)=(-284.754\ldots)/(-32)=8.89858\ldots \end{gathered}`

One of the results is negative, so it doen's make sence for this situation. So, the only solution is:

`t=8.89858\ldots\approx8.8986`

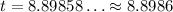
So, it take approximately 8.8986 seconds for it to hit the gournd.