Given:
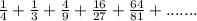
Required:
To find whether the given series is convergent or divergent.
Step-by-step explanation:
The given series is geometric series.
And the common ratio r is,
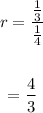
As
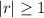
that means the terms do not tend towards 0, as

Therefore, the series is divergent.
Final Answer:
The given series is divergent, because the series is geometric and the absolute value of the common ratio is greater than 1.