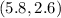You know that:

Since the DO is twice as long as OG, you can set up that:
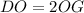
You can find the length of the segment DG by applying the formula to calculate the distance between two points:
![d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/be685jmxw05hm2tq94m5iuge2xjynn1hfn.png)
Then, if you set up that:
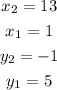
You get:
![DG=\sqrt[]{(13-1_{})^2+(-1-5)^2}=6\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/ijmis3ppe1gc5ktj3pshazaqanndvu4wr7.png)
Now you can set up that:
![\begin{gathered} DG=DO+OG \\ DG=2OG+OG \\ DG=3OG \\ \\ \frac{6\sqrt[]{5}}{3}=OG \\ \\ OG=2\sqrt[]{5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/c52drvv9hdqnv6l227yh5ltk1xjq86ue7d.png)
See the diagram below:
Then, using the information provided in the exercise and the values calculated, you can set up the following equation for the x-coordinate of the point O. By definition, the formula to find the coordinates of a point that is located between two points, that has a "r" proportion
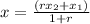
And for "y":
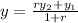
In this case, you know that:
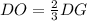
Then:
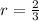
Therefore, substituting this value into each equation to find the coordinates of O, and evaluating, you get (remember to use the endpoints of DG):
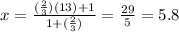
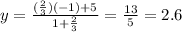
Then, the answer is: