Question

the jurassic zoo charged $11 for each adult admission and $8 for each child. the total bill for the 195 people from a school trip was $1713. how many children went to the zoo

Answer 1

Children : 144

Adults : 51

Step-by-step explanation

Step 1

Set the equations

let

x represents the number of children

y represents the number of adults

charge per child:8

charge per adult:11

total people:195

then

a)the total people is 195, so

`x+y=195\rightarrow equation(1)`

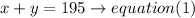
b) the total bill was $1713,so

total childrend +total adults=173

but,

total adults cost= rate*number of adults

total children cost= rate*number of childe

replacing

`8x+11y=1713\rightarrow equation(2)`

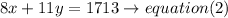
Step 2

solve the equations,

`\begin{gathered} x+y=195\rightarrow equation(1) \\ 8x+11y=1713\rightarrow equation(2) \end{gathered}`

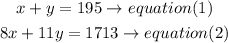
a) isolate the x value from equation 81) and replace in eqaution (2)

`\begin{gathered} x+y=195\rightarrow equation(1) \\ \text{subtract y in both sides} \\ x+y-y=195-y \\ x=195-y \end{gathered}`

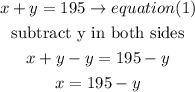
replace in equation (2)

`\begin{gathered} 8x+11y=1713\rightarrow equation(2) \\ 8(195-y)+11y=1713 \\ 1560-8y+11y=1713 \\ 3y+1560=1713 \\ \text{subtract 1560 in both sides} \\ 3y+1560-1560=1713-1560 \\ 3y=153 \\ \text{divide bothsides by 3} \\ (3y)/(3)=(153)/(3) \\ y=51 \end{gathered}`

therefore, the number of adults is 51

b) now, replace the y value into equation (1) to find x

`\begin{gathered} x+y=195\rightarrow equation(1) \\ x+51=195 \\ \text{subtract 51 in both sides} \\ x+51-51=195-51 \\ x=144 \end{gathered}`

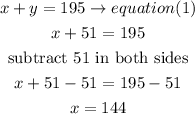
so, the number of children is 144

I hope this helps you