Question

Given the function -x^2 + x + 6 what is the horizontal distance between zeros?

Answer 1

The horizontal distance is 5

Step-by-step explanation:

The zeros of a function f(x) are the values of x which:

`f(x)=0`

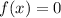
In this case, we have the function:

`-x^2+x+6`

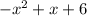
We want to find the zeros:

`-x^2+x+6=0`

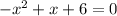
Now, we can use the quadratic formula:

`x_(1,2)=(-1\pm√(1^2-4(-1)6))/(2(-1))`
`x_(1,2)=(-1\pm√(1+4\cdot6))/(-2)`
`x_(1,2)=(1\pm√(1+24))/(2)`
`x_(1,2)=(1\pm√(25))/(2)`
`x_(1,2)=(1\pm5)/(2)`

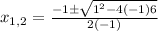
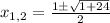
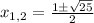
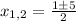
Then:

`\begin{gathered} x_1=(1+5)/(2)=(6)/(2)=3 \\ \end{gathered}`
`x_2=(1-5)/(2)=(-4)/(2)=-2`

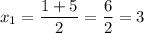
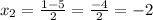
The two roots are x = -2 and x = 3

To find the distance, we take the absolute value of the difference:

`Distance=|-2-3|=|-5|=5`

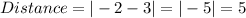
The distance is 5