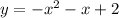Question

Write an equation for the quadratic graphed below: X-intercepts: (-2,0) and (1,0); y-intercept: (0,2)

Answer 1

The euqaion of a quadratic function is given by:

`y=ax^2+bx+c`

we need to find the values of the constants a, b and c. To do this we use the points given and plug the values of x and y in the equation above.

For the point (-2,0) we have that x=-2 and y=0; then we have:

`\begin{gathered} 0=(-2)^2a+(-2)b+c \\ 4a-2b+c=0 \end{gathered}`

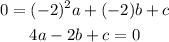
For the point (1,0) x=1 and y=0 then we have the equation:

`\begin{gathered} 0=(1)^2a+(1)b+c \\ a+b+c=0 \end{gathered}`

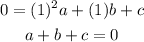
Finally for the point (0,2) x=0 and y=2 then we have the equation:

`\begin{gathered} 2=(0)^2a+(0)b+c \\ c=2 \end{gathered}`

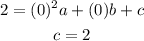
Hence we have the system of equations:

`\begin{gathered} 4a-2b+c=0 \\ a+b+c=0 \\ c=2 \end{gathered}`

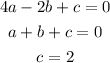
Now to solve this sytem we plug the value of c given by the third equation into the first and second equations to get:

`\begin{gathered} 4a-2b=-2 \\ a+b=-2 \end{gathered}`

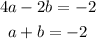
To solve this new system we multiply the second equation by 2:

`\begin{gathered} 4a-2b=-2 \\ 2a+2b=-4 \end{gathered}`

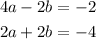
we add the equations:

`\begin{gathered} 4a-2b+2a+2b=-2-4 \\ 6a=-6 \end{gathered}`

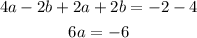
Now we solve for a:

`\begin{gathered} 6a=-6 \\ a=-(6)/(6) \\ a=-1 \end{gathered}`

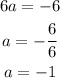
hence a=-1.

Finally to get b we plug the values of a and c in the first of our originals equations:

`\begin{gathered} 4(-1)-2b+2=0 \\ -4-2b+2=0 \\ -2b-2=0 \end{gathered}`

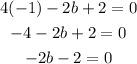
and solve for b:

`\begin{gathered} -2b=2 \\ b=(2)/(-2) \\ b=-1 \end{gathered}`

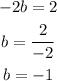
Hence b=-1.

Now that we have the values of the constant we have that the equation is:

`y=-x^2-x+2`