2(x²+1)(x+1)(x-1)
1) Let's examine that polynomial to check whether that polynomial can be factored or not.
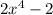
2) Examining we can see that the coefficient of the x-term (2) and the constant (2), are the same. So we can find the GCD, between 2,2 and write it as a factor.
GCD (2, 2) = 2
Now we'll divide every term by the GCD, and write it inside the parentheses just like this
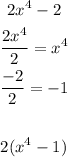
2.2) Now let's proceed with the factorization of the binomial x^4-1
Remembering that (a+n)(a-b)=a²-b²
Notice that we are dealing with a 4th-degree polynomial, so we can write it as:
So we can rewrite it as
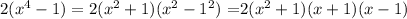
3) So our polynomial is not prime, for it can be reduced. And it can be written as 2(x²+1)(x+1)(x-1) in its simplest form.