SOLUTION
The equation of a line in slope intercept form is given as

Comparing this to

For two lines to be perpendicular, their product of their slope should be = -1
So we have
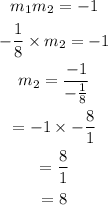
So the equation of the line becomes
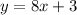
So the best choice should be one with slope of 8
If you bring 8x to meet y, we have
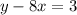
So the correct answer is the equation looking like this above
So the best answer is
y - 8x = -2, the last option is the answer