Question

Using the following equation, find the center and radius of the circle. You must show all work and calculations to receive credit.x2 −2x + y2 − 6y = 26

Answer 1

The center of the circle is (1, 3) and its radius is 6

Explanation

Given the equation:

`x^2-2x+y^2-6y=26`

we need to complete the square of the following expressions:

`\begin{gathered} x^2-2x \\ y^2-6y \end{gathered}`

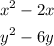
To do this we need to divide the coefficient of the x-term, which is -2, and the y-term, which is -6, divide them by 2, and then square them, that is,

`\begin{gathered} (-(2)/(2))^2=(-1)^2=1 \\ (-(6)/(2))^2=(-3)^2=9 \end{gathered}`

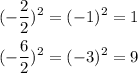
Adding 1 and 9 at both sides of the equation:

`\begin{gathered} x^2-2x+y^2-6y+1+9=26+1+9 \\ (x^2-2x+1)+(y^2-6y+9)=36 \\ (x-1)^2+(y-3)^2=36 \end{gathered}`

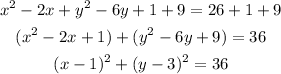
This equation has the form:

`(x-h)^2+(y-k)^2=r^2`

which is a circle centered at (h, k) with radius r.

Therefore, the center of the circle is (1, 3) and it radius is 6 (6² = 36)