We are given the relationship:
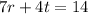
a. It's required to find a relationship where r is a function of t. To do that, we need to solve the equation for r.
Subtract 4t:
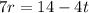
Divide by 7:
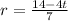
b. We use the function found in part a and evaluate it for t=-7:
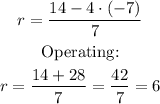
Thus, f(-7) = 6
c. Solve f(t) = 18
Again, we use the function from part a and solve the equation:
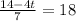
Multiplying by 7:
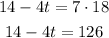
Subtract 14 and then divide by -4:
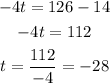
t = -28