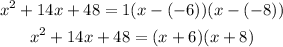Question

Please help me with problem so I can help my son to understand betterFactor.x^2+14x+48 Enter your answer in the box.

Answer 1

The polynomial:

`x^2+14x+48`

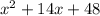
has the form:

`ax^2+bx+c`

with a = 1, b = 14, and c = 48.

This kind of polynomials can be factored as follows:

`ax^2+bx+c=a(x-x_1)(x-x_2)`

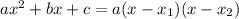
where x₁, and x₂ are the roots of the polynomial. We can find the roots of a quadratic polynomial with the help of the quadratic formula, as follows:

`\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{-14\pm\sqrt[]{14^2-4\cdot1\cdot48}}{2\cdot1} \\ x_(1,2)=\frac{-14\pm\sqrt[]{4}}{2} \\ x_1=(-14+2)/(2)=-6 \\ x_2=(-14-2)/(2)=-8 \end{gathered}`

Using a = 1, x₁ = -6, and x₂ = -8, the factored form is:

`\begin{gathered} x^2+14x+48=1(x-(-6))(x-(-8)) \\ x^2+14x+48=(x+6)(x+8) \end{gathered}`