We can picture the following situation:
imagine that instead of the places of the candelabra, you have 4 boxes (which represent the places in the candelabra).
Since Sally is arranging the candles from left to right, this means that the order matters. So we can have the following picture
Each number represents its position from left to right. To identify the total number of arrangements, we will use the fundamental principle of counting. This principle works as follows: To identify the total number of arrangements, we simply calculate the total number of available possibilites for each box and then we can multiply this numbers together.
So, we proceed. For the first box, since we haven't picked any candle, we have a total of 11 possibilites.
After picking one candle we have the following picture
Now, we want to fill the second spot. Since we already filled the first one, that means we have available 10 candles to choose. So, the total number of possibilities is 10.
Continuing in the same fashion, to fill box 3 we have a total of 9 possibilities and to fill the last box we have a total of 8 possibilities.
So, using the counting principle, the total number of possible arrangements is
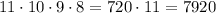
So, there are 7920 different ways in which Sally can arrange the candles in the candelabra