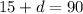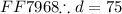Question

Challenge -- Find all of the missing angles - a, b, c, and d. L- ✓ b d 15 a а 60 55

Answer 1

The angels 60, a, and 55 are supplementary, meaning they add up to 180 degrees.

Therefore we have

`60+a+55=180`

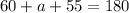
Solving for a gives us

`\textcolor{#FF7968}{a=65.}`

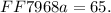
Now, we know that the sum of angles in a triangle is 180 degrees; therefore,

`a+b+90=180`

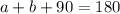
since a = 65, we have

`65+b+90=180`

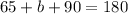
solving for b gives us

`\textcolor{#FF7968}{b=25.}`

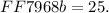
The angle c is opposite the angle b; therefore, it is

`\textcolor{#FF7968}{c=25.}`

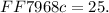
Angles d and 15 are complementary meaning they add up to 90; therefore, we have

`15+d=90`
`\textcolor{#FF7968}{\therefore d=75}`