In order to calculate the total surface area of this figure, let's consider the following views:
From above: 2 rectangles, one with dimensions 8 and 6 and one with dimensions 12 and 6.
From below: 1 rectangle with dimensions 20 and 6.
From the right: 2 rectangles, both with dimensions 6 and 4.
From the left: 1 rectangle with dimensions 6 and 8.
From the front and back: 2 composite figures, made by 2 rectangles each, one with dimensions 8 and 4 and one with dimensions 20 and 4.
So the total surface area is:
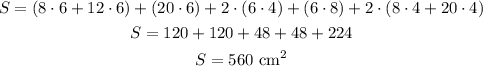
Therefore the surface area of the figure is equal to 560 cm².