Question

Consider the following data set: 23, 9, 8, 12, 21, 18, 14.What is the variance?A 5.398B 29.143C 15D 204

Answer 1

B. 29.143

Step-by-step explanation:

Given the set of data: 23, 9, 8, 12, 21, 18, 14

To find the variance, we follow the steps below:

Step 1: Find their mean.

`\begin{gathered} \text{Mean}=(23+9+8+12+21+18+14)/(7) \\ =(105)/(7) \\ =15 \end{gathered}`

Step 2: We subtract the mean from each of the values and square it.

`\begin{gathered} (23-15)^2=8^2=64 \\ (9-15)^2=6^2=36 \\ (8-15)^2=7^2=49 \\ (12-15)^2=3^2=9 \\ (21-15)^2=6^2=36 \\ (18-15)^2=3^2=9 \\ (14-15)^2=1^2=1 \end{gathered}`

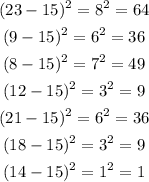
Step 3: We find the average of our results from step 2.

`\begin{gathered} \text{Variance}=(64+36+49+9+36+9+1)/(7) \\ =(204)/(7) \\ =29.143 \end{gathered}`

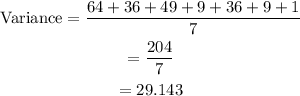
The variance is 29.143.