A generic line function is based on this format:
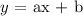
In this case, 2x + y = 5 we have to isolate 'y' to fill the format above:
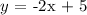
a = -2 and b = 5. So that is a linear function. I will show to you other examples that are not linear:
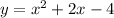
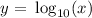
![y=\sqrt[]{x}](https://img.qammunity.org/2023/formulas/mathematics/college/z3kevgn2c29nk34ba6n3a5xhvm9rhyzg0b.png)
These are not linear functions because they are not in the y = mx + b format! m and b can be any real number. If m is equal to zero, the function will be constant! Otherwise, if b is equal to zero, the function will be linear.