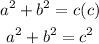With the triangles given:
Then, the proportion for first triangle and second triangle would be:
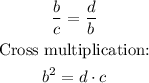
Proportin for first triangle and third triangle:
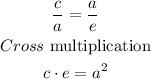
f. The equations would be:
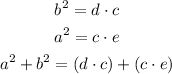
g. Then, factor out a common factor:
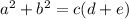
h. As a final step, replace the expression inside the parenthesis with one variable and then simplify: