Question

You are given the choice of taking the simple interest on $100,000 invested for 3 years at a rate of 5% or the interest on $100,000 invested for three years at an interest of 5% compounded monthly. Which investment earns the greater amount of interest? Given the difference between the amounts of interest earned bu the two investments.

Answer 1

Statement Problem: You are given the choice of taking the simple interest on $100,000 invested for 3 years at a rate of 5% or the interest on $100,000 invested for three years at an interest of 5% compounded monthly. Which investment earns the greater amount of interest? Given the difference between the amounts of interest earned bu the two investments.

Solution:

The simple interest of an amount invested P fot time t at a rate of r is calculated using;

`I=Prt`

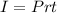
Thus, the interest is;

`\begin{gathered} P=100,000,r=0.05,t=3 \\ I=100000*0.05*3 \\ I=15000 \end{gathered}`

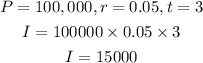
The interest earned using simple interest is $15,000.

The amount earned using compound interest is;

`\begin{gathered} A=P(1+(r)/(n))^(nt)_{} \\ P=100000,r=0.05,t=3,n=12(\text{monthly)} \\ A=100000(1+(0.05)/(12))^(12(3)) \\ A=116147.22 \end{gathered}`

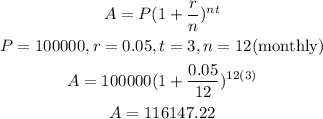
But the interest earned is the difference between the total amount earned and the invested amount. We have;

`\begin{gathered} I=A-P \\ I=116147.22-100000 \\ I=16147.22 \end{gathered}`

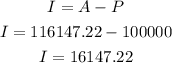
The interest earned using compound interest is $16,147.22

CORRECT ANSWER: The investment with the compound interest earns greater amount of interest.

The difference between the amounts of interest earned by the two investments is;

`16147.22-15000=1147.22`

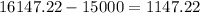
The difference between the amounts of interest earned by the two investments is $1,147.22