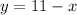Solution:
Given:
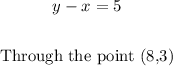
The first line given is y - x = 5
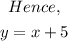
To get the slope of line 1, we compare the equation with the general equation of a straight line.
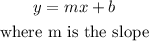
Thus,

The slope of line 1 is 1.
Since line 2 is perpendicular to line 1, then their slopes are negative reciprocals of one another.
This means the product of their slopes is -1.
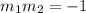
Hence, the slope of line 2 is gotten by;
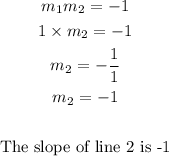
Hence, the equation of the perpendicular line through the point (8,3) will be;
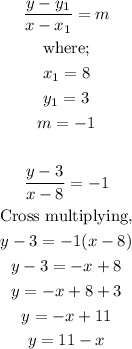
Therefore, the equation for the perpendicular line passing through the point (8,3) is;