Question

In the diagram below the mass on the incline is 4.0 kg and the hanging mass is 5.0 kg.The pully is frictionless and the string and pully are massless. The incline makes a 40°with the horizontal. The acceleration of the hanging mass is 1.50 m/s2. What is thetension on the string and the coefficient of friction between the incline and the mass onit?

Answer 1

Given:

The mass on the incline, m=4.0 kg

The hanging mass, M=5.0 kg

The angle of inclination, θ=40°

The acceleration of the masses, a=1.50 m/s²

To find:

The tension on the string and the coefficient of friction between the incline and the mass on it.

Step-by-step explanation:

As the pulley and the string is massless and the pulley is frictionless, the acceleration of both masses is the same. And the tension in both parts of the string is the same too.

Let us assume that T is the tension in both parts of the string.

The net force acting on the hanging mass is given by,

`F_M=Ma=Mg-T`

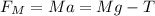
Where g is the acceleration due to gravity and T is the tension in the string.

On rearranging the above equation,

`\begin{gathered} T=Mg-Ma \\ =M(g-a) \end{gathered}`

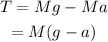
On substituting the known values,

`\begin{gathered} T=5.0(9.8-1.50) \\ =41.5\text{ N} \end{gathered}`

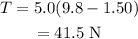
The net force on the mass on the incline is given by,

`\begin{gathered} F_m=ma=T-mg\sin\theta-f \\ =T-mg\sin\theta-mg\cos\theta\mu \end{gathered}`

Where f is the frictional force and μ is the coefficient of friction.

On rearranging the above equation.,

`\mu=(T-mgsin\theta-ma)/(mg\cos\theta)`

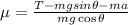
On substituting the known values,

`\begin{gathered} \mu=(41.5-4.0*9.8*\sin40\degree-4.0*1.50)/(4.0*9.8*\cos40\degree) \\ =0.34 \end{gathered}`

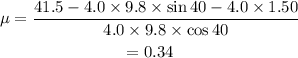
Final answer:

The tension in the string is 41.5 N

The coefficient of the friction between the incline and the mass is 0.34