Equation of a shaded region
We have the body line described by the equation:
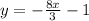
For the shaded region we have two possible cases:
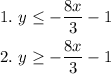
We select any point from the shaded region. This time we are going to work with the point (-3, -3), that is when x = -3 and y = -3.
We are going to replace it in the equation and after that we are going to complete it using one of the signs ≥ or ≤ using the one that gives as a true inequality:
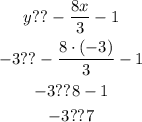
Since -3 is minor than 7, the sign we use is ≤:
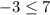
Then, we have this time the case 1.
Answer: The inequality that describes the shaded region is y ≤ -8x/3 -1
