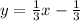Question

2. In the xy-plane above, ABCD is a square and point E is the center of the square. The coordinates of points C and E are (7,2) and (1,0), respectively. Write an equation of the line that passes through points A, E, and C. 6 2 C X A D

Answer 1

Given ABCD is a square

The coordinates of point C = ( 7 , 2 )

The coordinates of point E = (1 , 0 )

We need to find the equation of the line passing through the points A , E and C

The general equation of the required line is:

`y=mx+b`

Where m is the slope and b is a constant

the slope = Rise/Run

Rise = 2 - 0 = 2

Run = 7 - 1 = 6

Slope = 2/6 = 1/3

so,

`y=(1)/(3)x+b`

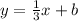
using the point E = (1 , 0 ) to find the value of b

when x = 1 , y = 0

`\begin{gathered} 0=(1)/(3)\cdot1+b \\ b=-(1)/(3) \end{gathered}`

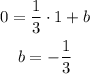
So, the equation of the line is :

`y=(1)/(3)x-(1)/(3)`