Answer and Explanation:
Given:
Part A: The equation for Triangle 2 is;
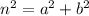
Part B: Since;
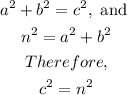
The resulting equation is c^2 = n^2
Part C: Let's take the square root of both sides from Part B;

The resulting equation is c = n
Part D:
By taking the square root in Part B we can see that side c and side n are equal in triangle 1 and triangle 2 respectively. So the equation is true.
Part E:
The relationship, c = n, shows that triangle 1 is also a right triangle because we have that side c is equal to the hypotenuse side n of the right triangle 2.