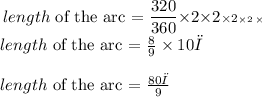Answer:
![\begin{gathered} Equation\text{ = }(\theta)/(360)\text{*2}*\text{\pi}* r \\ Equation\text{ = }(320)/(360)\text{* 2}*\text{\pi}*5 \\ \\ length\text{ of the arc = }(80π)/(9) \end{gathered}]()
Step-by-step explanation:
Given:
11) arc BC = 40°
highlighted arc = ?
radius = 5 in
To find:
the length of the highlighted arc
First we need to find the measure of the highlighted arc
highlighted arc + BC = 360°
highlighted arc + 40° = 360°
highlighted arc = 360 - 40
highlighted arc= 320°
The formula for length of an arc when the angle is in degrees:
![\begin{gathered} Length\text{ of an arc = \theta/360 * 2\pi r} \\ where\text{ r = radius} \\ θ=\text{ angle = highlighted arc} \end{gathered}]()
Substitute the values into the formula: