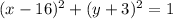Given the endpoints of the diameter are (16,-2) and (16,-4).
Find the center of the circle by finding the midpoint of the line segment joining (16, -2) and (16,-4).
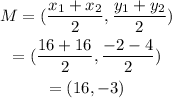
Now, find the radius of the circle using the distance formula.
![\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(16-16)^2+(-4-(-2))^2} \\ =\sqrt[]{(-2)^2} \\ =2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qwtzy742g9fzw6xb85g5t4g7q9rgd7fthx.png)
Thus, the diameter of the circle is 2. Hence the radius is 1 unit.
The standard equation of a circle is
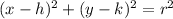
where (h, k) is the center and r is the radius.
Substitute the obtained values into the equation.