STP (Standard temperature and pressure) states that the temperature is 273 K (0°C) and the pressure is 1 atm.
To solve this problem, we have to find the number of moles of CO2. Based on the given data, we're going to find the number of moles using the following formula:
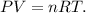
where P is pressure, V is volume, n is the number of moles, R is the ideal gas constant (0.082 atm*L/mol*K) and T is the pressure. Let's solve for 'n' and replace the data that we have (The pressure is 1 atm, volume is 179.2 L and T is 273 K):

The next step is to see how many moles of NaCl are forming by 8 moles of CO2. You can see in the chemical reaction that there are 2 moles of NaCl produced with 1 mol of CO2. The calculation would be a rule of three, like this:

And the number of moles would be:
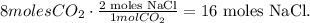
There are 16.0 moles of NaCl formed, the answer would be (2).