Question

27. How long will it take to double an investment at 4.9% compounded continuously? Round your answer to the nearest tenth of a year.

Answer 1

Recall that to calculate the amount after t years that is compounded continously at a intereset rate r of an investment of a principal P is given by the formula

`A=Pe^(rt)`

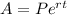
In this case, the initial amount is P. Since we want to calculate the value of t for which A is exactly 2*P we have the equation

`2P=Pe^(rt)`

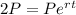
we know that r=0.049 and we want to solve this equation for t. WE start by dividing both sides by P. So we get

`2=e^(0.049t)`

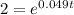
If we apply the natural logarithm on both sides, we get

`0.049t=\ln (2)`

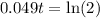
so if we divide both sides by 0.049, we get

`t=(\ln (2))/(0.049)=14.14145860`

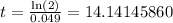
which rounded to the nearest tenth of a year is 14.1 years