Given:
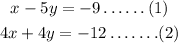
Let's check the ordered pair (-4,1) in the first equation
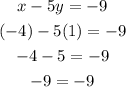
Hence, (-4,1) is the solution of the first equation.
Now, check (-4,1) in the second equation
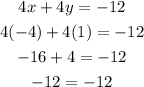
So, (-4,1) is the solution of the second equation.
Hence, (-4,1) is the solution of both systems of the equation.