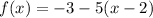Given the graph of the function:
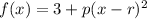
From the graph of the function:
Vertix = (2, q)
The y-intercept = (0, 23)
We will find the values of p, q, and r
From the point of the vertex of the graph: r = 2, q = 3
And from the point of the y-intercept
When x = 0, f(x) = 23 and substitute with r
so,
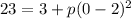
Solve the equation to find p
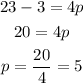
so, the answer of part A:
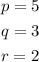
b) if the graph is reflected about to y-axis, write the equation of the curve
So, the equation of the function will be:

simplifying the equation
So,