Question

Can you please help me

Answer 1

y = 4.62

x = 2.31

Explanation:

The cosine ratio for 30 degrees gives

`\cos 30^o=(4)/(y)`

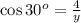
multiplying both sides by y gives

`y\cos 30^o=4`

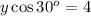
Finally, dividing both sides by cos 30 gives

`y=(4)/(\cos 30^o)`

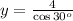
Since

`\cos 30^o=\frac{\sqrt[]{3}}{2}`

The above gives

`y=\frac{4}{\frac{\sqrt[]{3}}{2}}`
`\boxed{y=\frac{8\sqrt[]{3}}{3}\approx4.62.}`

Now we find the value of x.

The tangent ratio for 30 degrees gives

`\tan 30^o=(x)/(4)`

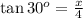
multiplying both sides by 4 gives

`x=4\tan 30^o`

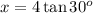
Now since

`\tan 30^o=\frac{\sqrt[]{3}}{3}`

the above gives

`x=4\cdot\frac{\sqrt[]{3}}{3}`
`\boxed{x\approx2.31.}`

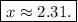
Hence, to summarize

y = 4.62

x = 2.31