Question

Eric drops a 2.30 kg water balloon that falls a distance of 35.65 m off the top of abuilding. What is the kinetic energy at the bottom?

Answer 1

Givens.

• The mass of the ballon is 2.30 kg.

,

• The height is 35.65 m.

First, find the final velocity when the balloon is at the bottom. Use a formula that relates height, initial speed, final speed, and gravity.

`v^2_f=v^2_0+2gh`

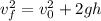
Where

• v_0 = 0 because the balloon starts from rest.

,

• Gravity is g = 9.8 m/s^2.

,

• h = 35.65 m.

Use all these magnitudes to find the final velocity v_f

`\begin{gathered} v^2_f=0^2+2(9.8\cdot(m)/(s^2))(35.65m) \\ v^2_f=698.74m^2 \\ v_f=\sqrt[]{698.74m^2} \\ v_f\approx26.4((m)/(s)) \end{gathered}`

Once we have the velocity at the bottom, find the kinetic energy using its formula.

`K=(1)/(2)mv^2`

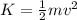
Where m = 2.30 kg, and v = 26.4m.s.

Therefore, the kinetic energy at the bottom is 801.5 J.