Question

Rd Find the 63 term of the following arithmetic sequence. 14, 20, 26, 32,

Answer 1

Find the 63 term of the following arithmetic sequence. 14, 20, 26, 32

we have

a1=14

a2=20

a3=26

a4=32

so

a2-a1=20-14=6

a3-a2=26-20=6

a4-a3=32-26=6

therefore

the common difference d=6

The general equation for an arithmetic sequence is equal to

`a_n=a_1+d(n-1)`

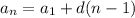
we have

a1=14

d=6

substitute

`\begin{gathered} a_n=14+6(n-1) \\ a_n=14+6n-6 \\ a_n=8+6n \end{gathered}`

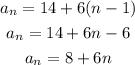
find the 63rd term

For n=63

substitute in the formula

`\begin{gathered} a_n=8+6(63) \\ a_n=386 \end{gathered}`

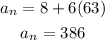
the answer is 386