Question

Can you please explain in a easy way please? Where I can understand step by step? Thank you!

Answer 1

A piecewise function is a function built from pieces of different functions over different intervals; in this case we have a piecewise function defined by two pieces.

The first piece tells us that if x is any value less than or equal to 3 the we need to use the expression 2x for the function.

The second piece tells us that if x is any value greater than 3 we have to use the expression:

`(1)/(3)x^2-2x+9`

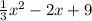
Now, to graph this function we need to make a table of values like any other function taking into acount on which interval is x in orther to use the proper expression for the output of the function:

In this table we use what we stated above; for example since 0 is less than 3 we have to use the expression 2x, then we have:

`f(0)=2(0)=0`

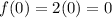
and so on for the values one, two and three.

For the other values we notice that they are greater than 3 then we hace to use the second expression, for example:

`\begin{gathered} f(4)=(1)/(3)(4)^2-2(4)+9 \\ f(4)=(16)/(3)-8+9 \\ f(4)=5.33\bar{3}-8+9 \\ f(4)=6.33\bar{3} \end{gathered}`

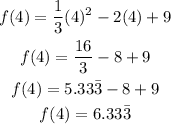
and so on for any value greater than 3.

Now we plot this points and join them to get the graph: